Time - Varying Rates of Returns

The only difference is that $$1 + r_0 \neq (1 + r)^t $$ $! NPV = C_0 + \frac{C_1}{(1 + r_{0,1})} + \frac{C_2}{(1 + r_{0,2})} + \frac{C_3}{(1 + r_{0,3})} + \cdots $!

Here, we have : $! 1 + r_{0,2} = (1 + r_{0,1})(1 + r_{1,2}) $! etc etc…

Why do we have time varying Rates of returns?

In the real world, obviously interest rate differ through time. Long term bonds usually offer different annual interest rate than short - term bills. Will return to this later.

Q1 : If the 1 - year interest in year 1 is 5%, and the 1 - year interest in year 2 is 3%, what is the annualized interest rate?

$! \begin{aligned} r_{0,1} &= 0.05\\ r_{1,2} &= 0.03 \\ 1 + r_{0,2} &= 1.05 \times 1.03 \\ r_{0,2} &= .0815 \\ \text{annualized : } r_{\bar{2}} &= \sqrt{1 + r_{0,2}} - 1 \\ &= about 4\% \end{aligned}$!

Geometric average (annualized interest rate:)

is geometric average of interest rates. $$ \rarr $$ equivalent to saying that “with that interest rate, you will same interest rate as calculated otherwise”

Arithmetic average is always greater than annualized interest rate. Also, almost all interest rates are quoted in annualized terms.

So why do we have different interest rate? Inflation:

• Real and Nominal rate : A real dollar always has the same purchasing power.
• In real world, most contracts are in nominal terms.

Q2 : If you have $100, and you will have $10 next year, and you can purchase 50 bread today, and bread will be 4%% more expensive next year: your purchasing power only increases by 5.77 %, not 10%.

The inflation adjustment formula:

$! (1 + 0.0577) * (1 + 0.04) = 1 + 0.10 $!

Never mix nominal cash flows with real rates

Q3 : If a project will return $110 in nominal, and cost of capital is 10%, PV is? $! PV = \frac{110}{1 + 0.1} = \$ 100 $!

Q4 : If the inflation rate is 4%, and a project will return $110 in nominal cash next year, then what is the purchasing power of this future $110 in today’s dollars?

$! \frac{\$ 110}{1 + 0.04} = 105.77 $!

Q5.1 : (amalgam of Q3, Q4) If the inflation rate is 4%, and the cost of capital is 10%, real cost of capital:

$!\begin{aligned} ( 1 + real) ( 1 + \pi) &= (1 + nominal)\\ (1 + r)(1 + 0.04) &= (1 + 0.1)\\ r &= 5.77 \% \end{aligned} $!

Q5.2 : What is the project’s real dollar value discounted by the real cost of capital? Why?

$! PV = \frac{105.77}{1.0577} = \$ 100 $!

The Yield Curve and US Treasuries:

• US Treasuries are the most important financial security.
• Annual trading is $100 ~ $150 trillion.
• Market is almost perfect.
  • Low transaction costs
  • Few opinion differences
  • Deep market (many buyers and sellers)
• Almost no uncertainty about repayments

Yield Curve:

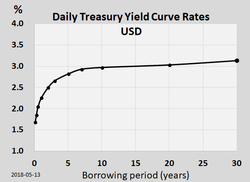
The longer the borrowing period, the greater the annualized rate of return(usually, not always)

The yield cure is fundamental tool of finance. It always graphs annualized rates. It measures differences in the costs of capital for risk - free projects with different horizons.

• Spot interest rate : Interest rate that starts today : $$r_{0,1}$$
• Forward rate : Interest rate in the future $$r_{1,2}$$

More notation

• We denote annualized interest rate as $$r_{\overline{15}}$$ (for case of 15 years). This is different from $$r_{0,15}$$, as the later is 15 - year non - annualized interest rate

So why do we have upward - sloping yield curve?

A. Higher future inflation? B. Higher future interest rate? C. Risk Compensation?

• Risk premium : Need greater return for longer term flows.

This is also why we have to think of time - variant rate of return.

When we are considering NPV, we have to think of something like upward - sloping discount rate.

• This also means that the fact that longer term projects have to offer higher rates of return not only because of higher risk, but also because of preference. US treasury bond has almost no risk, but has upper sloping rates of return.
• Of course, long - term projects are also riskier.